oi wiki原文:链接
洛谷例题:链接
引入

构造格雷码
我们先来讲一下构造的方法再讲为什么吧。不然除非你拥有发明这种算法的实力。。
大佬当我什么都没说(好像大佬也刷不到这个蒟蒻的blog
手动构造
k 位的格雷码可以通过以下方法构造。我们从全 0 格雷码开始,按照下面策略:
翻转最低位得到下一个格雷码,(例如 000\to 001);
把最右边的 1 的左边的位翻转得到下一个格雷码,(例如 001\to 011);
交替按照上述策略生成 2^{k-1} 次,可得到 k 位的格雷码序列。
为什么这么做呢?就相当于十进制1 ~ 2^k, 把每一位转化成对应格雷码就是这样了。
那为什么十进制这么转化成格雷码?请看下文正确性证明。
镜像构造

这个方法是我最推荐的,最为简单的。
他原文是这样的:“k 位的格雷码可以从 k-1 位的格雷码以上下镜射后加上新位的方式快速得到”
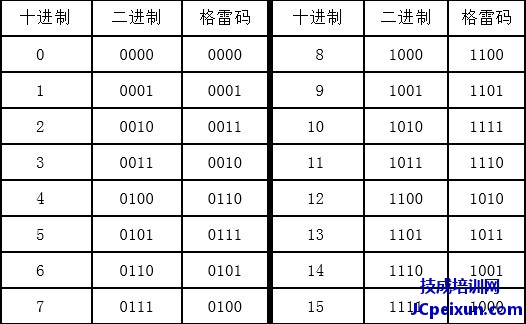
人话来说,就例如图片里k = 2编程k = 3,就把k = 2的格雷码先照搬过来,再把它反着写一遍跟在原来的后面,最后原来的前面加个零0后面的加一个1,就变成k = 3的格雷码了。
原理:蒟蒻也不知道诶,可能就是单纯的找规律吧~(试图萌混过关
格雷码转二进制

看不懂?很正常。因为我也看不懂。。。太抽象了。
直接看代码也许还会好理解一点怎么做:
int g(int n) { return n ^ (n >> 1); }
代码很简单吧?假设二进制1011要转换成对应格雷码,就右移一位(除以2)并与其异或。
大概是这样的:
1011 -> 101
101 ^ 1011 = 1110
正确性证明
关于这个我专门录了一期视频,个人感觉还是讲的挺详细的,可能有的时候结巴了一点(对不起
讲解视频
然后OI WIKI上的解释是这样的:

很抽象,建议看我视频然后点赞的说(企图萌混过关
例题
洛谷例题
#include <bits/stdc++.h>
using namespace std;
unsigned long long n = 5, k;
int main() {
cin >> n >> k;
k ^= k >> 1;
for (int i = n - 1; i >= 0; i--) {
cout << (k>>i&1);
}
return 0;
}
当然题解第一篇是最优解,但我觉得这样好理解一些。
首先,输入n,k,再讲十进制k转换为对应的格雷码
然后,从n-1位到第0为遍历输出
最后就没有啦,很简单把.^.
如果有不理解的地方那应该只能是k转换为格雷码,那么建议看一下我的15min视频.^.
再见啦~本文用一个星期零零散散地写完,希望大家喜欢
